「水産政策の改革」が提案する資源管理の問題点
櫻本和美(23漁大)
1. はじめに
2018年12月8日、第197回臨時国会で、改正漁業法が可決成立しました。漁業権付与の優先順位を廃止、海区漁業調整委員会委員の公選制廃止、最大持続生産量(MSY)に基づく数量管理を重視した個別割当(IQ)制度への移行など、改正漁業法は日本の漁業を根元的に変える可能性を内在しています。しかし、「70年ぶりの漁業法の大改正」をうたっている割には、国会での審議時間は衆院で13時間50分、参院で8時間45分と極めて短く、また、2018年6月に改正案が公表されるまで、改正案の具体的内容を知っている人はほとんどいない状況でした。改正漁業法は極めて非民主的なプロセスのもとで成立させた法案の1つとして、その名を歴史に残すことになるでしょう。当然のことながら各方面から厳しい批判が現時点においても噴出し続けています。批判の具体的内容については、他の著作を参照していただくことにして、ここでは資源の数量管理に焦点を絞って問題点を述べることにします。
2. 「水産政策の改革」が提案するMSYベースの資源管理はなぜダメか?
「水産政策の改革」ではMSYに基づく資源管理の実施が提案されています。「MSYとはある親の量に資源を維持しておけば、毎年毎年最大の漁獲量が得られる」という理論です。MSYは親と子の量的な関係(再生産関係といいます)から推定されます。水産庁が資源管理のお手本と崇拝するEUでも「再生産関係に基づいてMSYを推定する」ことが明記されています(水産庁ホームページ)。しかしながら、「親と子の量的関係が果たして存在するのか」が、今大きな問題になっています。
シュカルスキーら1)は、224にもおよぶ系群注1)の再生産関係を調べ、「85%の系群で、子の数は親の量によっては決まらず、環境による影響のほうがはるか大きい」ことを示しました。このことは、224系群中のほとんどの系群で「親と子の量的な関係が認められない」ということであり、「親と子の関係が認められないデータからMSYを推定することは原理的に不可能である」ことを示しています。
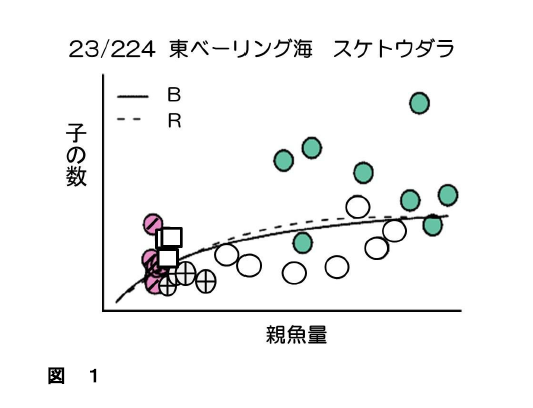
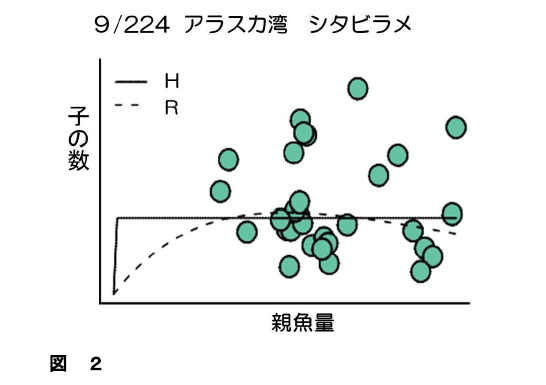
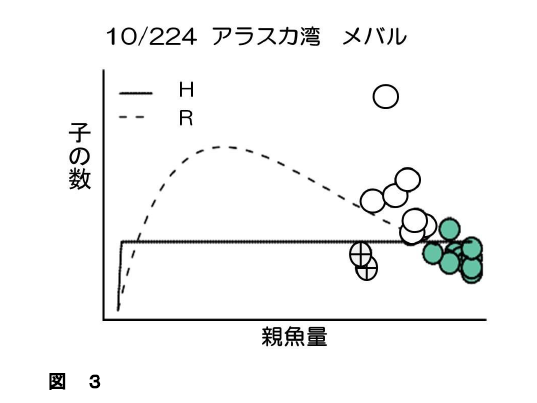
ところで、シュカルスキーら1)が示した224系群の再生産関係注2)は、図1、図2、図3のように3つパターンに分けることができます。図1のように増加傾向が認められるのが224系群中15%あり、約70%が図2のような無相関、約15%が図3のような減少傾向を示します。これらの図をみると、資源研究者がなぜ、親の量をコントロールすることによって、子の数がコントロールできると考えるのか、全く理解不能なことが分かります。「親と子の関係が認められない」のに、親の量をこの水準にしておけば、子の数はこうなるなどと言えるはずがありませんからね。注3)シュカルスキーら1)の研究は 「MSYの考え方を支持するデータは実際には存在せず、MSYも存在しない」ということを、実データを用いて示したことになります。
しかし、不思議なことに、図2のように親と子の関係が全く認められないデータや、図3のようにリッカーモデルやホッケー・スティックモデルが妥当であるなどとはどう間違えても言えそうにないデータから、まるで手品のように、MSYは推定されています(水産庁ホームページ)。では、実際にどんな方法でMSYを推定しているのかというと、「実データからはその妥当性が検証できない架空の資源変動モデル(リッカーモデルやホッケー・スティックモデルのことです)を仮定して、これまでその存在が論証されたことなどない架空のMSYなるものを無理やり推定してしまっている」ということです。そんな架空の資源変動モデル、架空のMSYに基づいて資源管理を実施しても、資源管理が成功することなどあり得ないと誰もが思いますよね。注4)その考えは正しくて、事実、水産庁がお手本とするEUの資源管理の実情を見ても、
186系群中なんと108系群(58%)が乱獲状態にあることが、どういう訳かちゃんと水産庁のホームページに掲載されています。そのような事実を無視して、なぜ水産庁がEUをお手本にしたがるのか全く理解できないのは私だけでしょうか?
3. 新しい資源変動理論
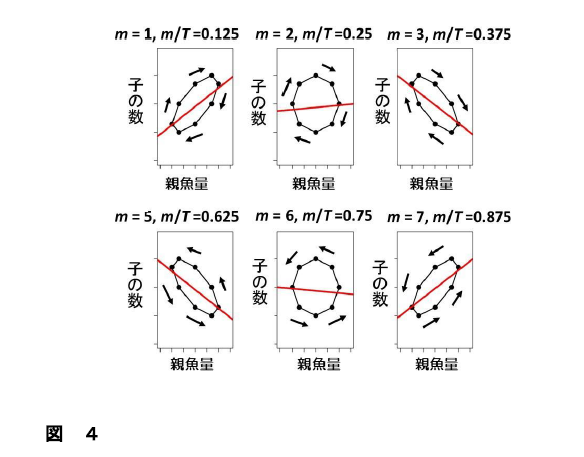
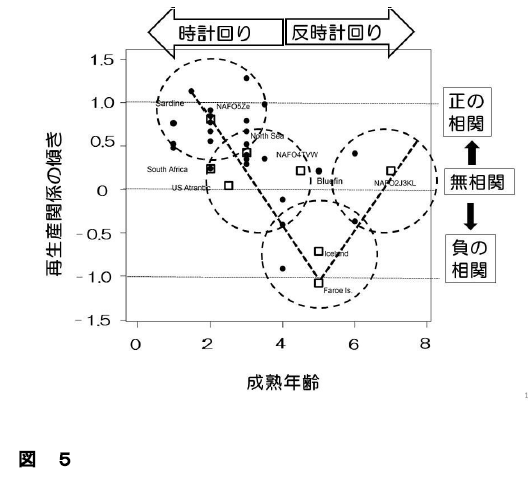
資源管理を真に成功に導くためには、架空の資源変動モデルではなく、正しい資源変動理論に基づき妥当と考えられる資源管理を実施することが何よりも大切であることは言うまでもありません。MSY理論に代わる新しい資源変動理論も既に提案されています2)。正しい資源変動理論では「子は親の量と環境変動によって決まる」とし、「85%で再生産関係は不明」とするシュカルスキーら1)とも見解は異なっています。正しい資源変動理論では「①再生産関係は増加、無相関、減少の3パターンに分類可能で、それぞれが時計回り反時計回りの2パターンを持つので、計6パターンに分類できる。②そのうちのどのパターンになるかは、環境変動の周期と、成熟年齢(平均成熟年齢)の比によって決定される」ことが明らかにされています(図4)。さらに、国内外の32系群について再生産関係の傾きと成熟年齢の関係を調べ、上記理論の正当性も示されています(図5)3)。
4. ガラパゴス化する水産資源研究
今年(2019年)2月、私は資源管理に関連する講演会に参加していました。講演会終了後、一人のジャーナリストの方が私のところにやって来て、「先生には大変失礼だけれども、資源学って本当に科学と言えるんですか?」と質問しました。まともな方なら、このような疑問を持たれて当然だと私も思っていたので、「事実を決して認めようとはしない水産資源学は科学などとはとても言えません」と答えました。日々命がけで漁業に従事されている漁業者の方はもちろん、漁業に直接関係のない一般の方々でも、まともな思考力のある人でMSYを信じている人などいないだろうと私は思います。まさに、「MSYとは資源研究者の間だけで通用する都市伝説」と言っても過言ではないでしょう。よく、「試験管の中の酵母菌の成長を調べた結果からMSYが正しいことは既に証明済みである」と真顔で主張する研究者がたまにいますが、この研究者は海の中と密度以外のすべての条件を一定にした試験管の中とでは、条件が全く違うことに、どうやら気が付いていないようです。MSYが海洋の水産資源に対して成り立つことが証明されたことなど一度としてないのですから… 4)。
ある資源研究者は「MSYは物理理論のようにものごとの挙動を正確に予測できるようなものではない。
…単なる概念である」と述べています5)。「MSYが科学ではない」ことを自ら認めるような驚くべき発言ですが、「MSYが概念」なら、実際の資源管理においても、その「概念」だけを用いるべきではないでしょうか?「MSYを推定し、MSYを達成する資源水準を管理目標とした漁獲可能量(TAC)を設定し注5)、TACを超過した漁業者は犯罪者として刑事罰を科す」という制度になっているのに、いくら何でも「MSYは単なる概念である」はないでしょう。「単なる概念」で犯罪者にされてしまう漁業者の身にもなってほしいものです。
事実を決して認めようとしない資源研究(外国も含む)は科学の世界から孤立し、ますますガラパゴス化していくことになるでしょう。「水産資源研究者による、水産資源研究者のための、水産資源研究」であってはならないと強く思う次第です。(東京海洋大学名誉教授)
文献
1) Szuwalski et al. Examining common assumptions about recruitment: a meta-analysis of recruitment dynamics for worldwide marine fisheries. Fish and Fisheries 16 (2015)
2) 櫻本和美. マグロ類資源の管理の成功に向けて―MSY理論に代わるべき新しい資源変動理論―水産振興605.(2018)
3) Sakuramoto, K. Are 20% B 0 , 20% B unfished , and B MSY Valid as Reference Points for Fisheries Resource Management? Open Access Library Journal, 4 (2017).
4) 櫻本和美. 生態学における密度効果という“幻想”アクアネット. (2014)
5) 市野川桃子:新たな資源管理目標.水産海洋学会シンポジウム要旨集(2019)
図の説明
図1 増加傾向を示す再生産関係(224系群中の23番目の系群を例として示した)。環境が同じであると見なせる同じレジーム内の点は同じ記号で示してある。B, R は、親と子の関係を表す代表的なモデルとしてよく知られているべバートン・ホルトモデル、リッカーリモデルをそれぞれ示す。親の増加に伴い子も増加しており、べバートン・ホルトモデルやリッカーリモデルをあてはめるのが妥当であるか否かも大きな疑問である 4)。
図2 無相関となる再生産関係(224系群中の9番目の系群を例として示した)。H, R は、親と子の関係を表す代表的なモデルであるホッケー・スティックモデル、リッカーリモデルをそれぞれ示す。親が少ないところのデータがなく、ホッケー・スティックモデルやリッカーリモデルをあてはめても全く意味がない。データのある範囲を見ると全くの無相関であり、親の増加に伴い子が増加するとか、親の増加に伴い子が減少するなどといった傾向は全く認められない。しかし、実際にはこのようなデータに、図中に示したようなホッケー・スティックモデルやリッカーリモデルをあてはめ、MSYを推定している。そして、「MSYを達成するためには、この資源水準に資源を維持すべきである」と主張するわけですから、とても科学的などと言えるレベルではない。この図を見て、「ある資源水準に資源を維持したらMSYが達成できる」などということを信じる人が果たしているのだろうか?
図3 減少傾向を示す再生産関係(224系群中の10番目の系群を例として示した)。H, R はあてはめたホッ
ケー・スティックモデル、リッカーリモデルをそれぞれ示す。この図を見て、親の量が多いところではリッカーリモデルによくあてはまるなどと思ってはいけません。そんなことを言う資源学者がもしいたら、似非資源学者だと思って間違いありません。「統計学で何かを語ることができるのはデータがある範囲に限る」というのが、統計学の基本中の基本です。データが全くない範囲も含めて「リッカーモデルが当てはまるだの、ホッケー・ステックが当てはまる」などということは全くもってナンセンス。このデータから言えることは、「親の増加に伴って子は減少する傾向がある」ということだけです。しかし、このような状態はたまたま偶然に出現したのもではなく、必ず出現することに注意する必要があります(224系群中15%ぐらいはこの状態です)。「親が多いほど子は少ない」なんて、生物学的におかしいですよね。リッカーリモデルやホッケー・スティックモデルなど既存の親子関係を表すモデルで、このような現象を説明することは全く不可能です。換言すると、実際の親子関係を表すデータで、リッカーモデルやホッケー・スティックモデルなどの既存の親子関係を表すモデルに合致するデータはほとんどなく、逆に、その反例を示すデータならいくらでも山ほどあるということです。
図4 子の数は環境変動の影響を受け周期8年のコサインカーブで表される周期変動をし、産卵親魚は成熟年齢分(m)だけずれて、同じ周期変動をしていると仮定したときのシミュレーション結果。成熟年齢が周期の半分(4年)より小さいと再生産関係の軌道は時計回りで、再生産関係の傾きは、m=1 の時は正、m= 2 の時は0(無相関)、m=3 の時は負となる 注5) 。成熟年齢が周期の半分(4年)より大きくなると再生産関係の軌道は反時計回りとなり、再生産関係の傾きはm=5 の時は負、m=6 の時は0(無相関)、m=7 の時は正となる。詳細は文献2を参照してください。
図5 日本沿岸および海外の32系群について再生産関係の傾きと成熟年齢の関係を示したもの。●は日本沿岸の系群のデータ、□は海外の系群のデータをそれぞれ示す。成熟年齢が小さい時は再生産関係の軌道は時計回りとなり、成熟年齢が増大するにしたがって再生産関係の傾きは正からゼロ(無相関)、負へと変化する。さらに、成熟年齢が大きくなると、今度は再生産関係の軌道は反時計回りとなり、成熟年齢の増大に伴って再生産関係の傾きは負からゼロ(無相関)、正へと変化する。ただし、環境変動の周期は、海域によっても年代によっても異なるので、それぞれの系群ごとに環境変動等についての詳細な分析を行う必要がある点には注意する必要がある。
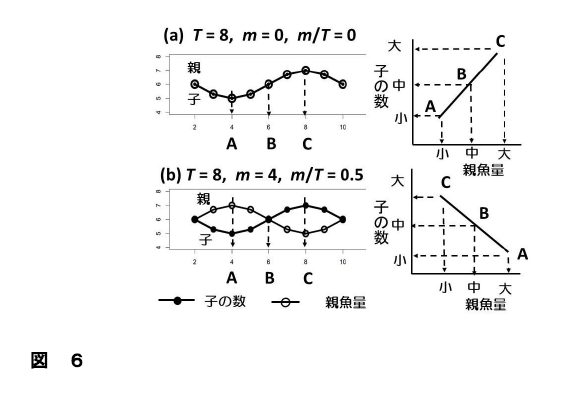
図6 資源変動の周期と成熟年齢の比(m/T)と再生産関係のパターンとの関係(a)は成熟年齢が0(すなわち、m/T=0 )の場合、(b)は成熟年齢が周期のちょうど半分の4歳の場合(すなわち、m/T=0.5)を示す。
注1)系群とは資源変動の単位、同じ魚種でもいくつかの系群に分かれる。例えば、日本沿岸のマイワシ
も、マイワシ太平洋系群とマイワシ対馬暖流系群の2つの系群に分けられ、それぞれ別々に資源変動
が分析されている。
注2) https://onlinelibrary.wiley.com/doi/abs/10.1111/faf.12083 のURL に行き、
Supporting information をプルダウン+クリックすると224 系群すべての再生産関係を見ることが
できる。
注3)メルマガ106号「マグロ類の資源管理の致命的問題点」も併せてお読みいただければと思います。
ここで説明したことと全く同じことが、マグロ類の資源管理でも行われています。すなわち、
親子関係が全く不明であるにも関わらず、架空の再生産モデル(べバートン・ホルトモデルやホッ
ケー・スティックモデル)を用い、架空のMSYを推定し、誤った管理が実施されていることが、体重
と罹患率のたとえ話を用いて解説されています。
注4)佐藤力生氏のブログ「本音で語る資源管理」7月7日版(http://shigenkanri.jp/?p=2224)「新た
な資源管理に基づく資源管理目標案等に科学的正当性はあるか?」も併せてお読みいただければと思い
ます。
注5)なぜ、環境変動の周期(T)と成熟年齢(m)の比(m/T)によって、再生産関係の傾きが正になった
り負になったりするのか?子の数は環境変動の影響を受け周期8年のコサインカーブで表される周期変
動をし、産卵親魚は成熟年齢分(m)だけずれて、同じ周期変動をしていると仮定した場合を例に
説明する。図6(a)は成熟年齢が0(すなわち、m/T=0)の場合で、この場合には子の変動と親魚量
の変動は完全に一致する。従って、m/T=0の場合の再生産関係を描くと年Aでは親も子も少なく、年B
では親も子も中ぐらい、年Cでは親も子も多いという状態になるため、再生産関係の傾きは図6の右の図
に示したように1になる(正の値)。これに対し、図6(b)は成熟年齢が周期のちょうど半分の4歳の
場合(すなわち、m/T=0.5)を示し、親の変動と子の変動がちょうど真逆になる。すなわち、年Aで
は親魚量は多にもかかわらず子は少なく、年Cでは親魚量は少ないにもかかわらず子は多い、という関
係になる。従って、m/T=0.5 の場合の再生産関係を描くと年Cでは親が少ないにもかかわらず子は多
く、 年Aでは親が多いにも関わらず子は少ない(年B では親も子も中ぐらい)という状態になるため、
再生産関係の傾きはマイナス1(負の値)になる。すなわち、m/T=0.5より小さい場合は、m/Tが
0.0 に近いと正の傾きを、m /T = 0.25に近いと0 に近い傾きを、m /T = 0.5に近いと負の傾きを持つ
(m/T=0.5より大きくなった場合や、なぜm/Tが0.5より小さいと軌道が時計回りになり、m/Tが0.5よ
り大きいと反時計回りになるのか等々についての詳細は文献2をご参照ください)。









